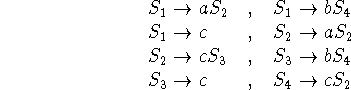Introduction

  The problem domain considered is a subset of the more general problem of construction of the grammar, of any type, that will accept a given set of strings. Though the language is restricted to the acceptance by a DFA it finds a broad application area, especially in NLP.

It is known that a DFA's can be expressed as regular grammars so the outcome of the proposed method will be a regular grammar, in particular a right-linear grammar. A grammar is said to be right-linear iff each production in P is of the form or where A and B are in and x is in .

Since the equivalence of NFA and DFA is trivial there will always exist a DFA for any set of strings acceptable by any NFA. So searching for a DFA will not be restrictive in the FA domain.

The state transition function of a DFA can be expressed as a matrix in which the columns are corresponding to the input symbols and the rows are corresponding to the different states. An element of the matrix in row s and column t represents the new state the automaton will be in if it was in the state s and the current input symbol t that was under the input head is consumed.

Here is an example, consider the following DFA:

 
Figure 1:   Example DFA

The matrix that corresponds to the state transition function of this DFA is:

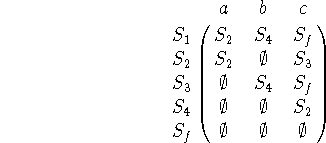
The grammar that will emerge from this DFA is: