Homework 3

Trapezoidal Cell Decomposition and Coverage

Introduction

This report will cover implementation and observations of trapezoidal cell decomposition and coverage of a robot in a polygonal environment.

In this homework, we use trapezoidal cell decomposition which divides free space into cells. Using trapezoidal cells, we can construct an adjacency graph which can be used for both navigation of a robot and coverage. Coverage of robot means that determining a path that passes over all points in a free space.

You can try these algorithms interactively:

Trapezoidal Cell Decomposition

We apply cell decomposition method on a 2D polygonial environment consisting of non-intersecting polygonal obstacles and a polygonal boundary. You can see that on the following figure. Obstacles are colored as blue and there is polygonal boundary includes all polygons. For the sake of simplicity, we assume also that each vertex on the polygons has distinct x coordinate. .


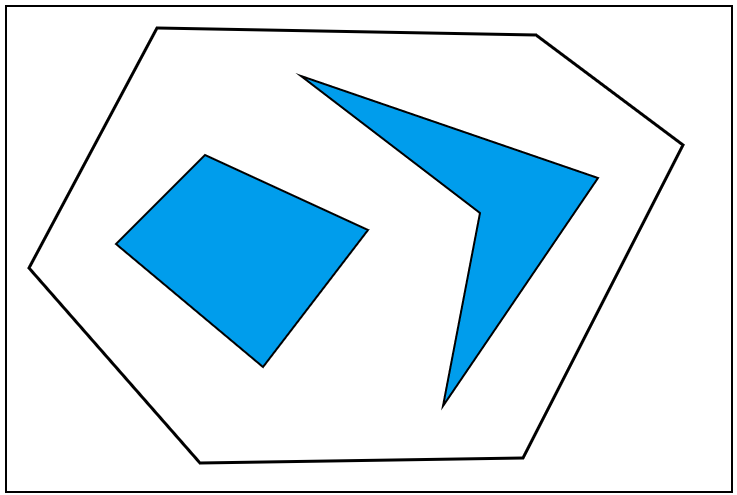
Figure 1-Polygonial Environment consists of 2D trapezoid-like shapes

Then polygon points are selected and marked as yellow circles. Note that polygons are ordered according to their position on x-axis. Actually this makes adjacency computations more efficient.


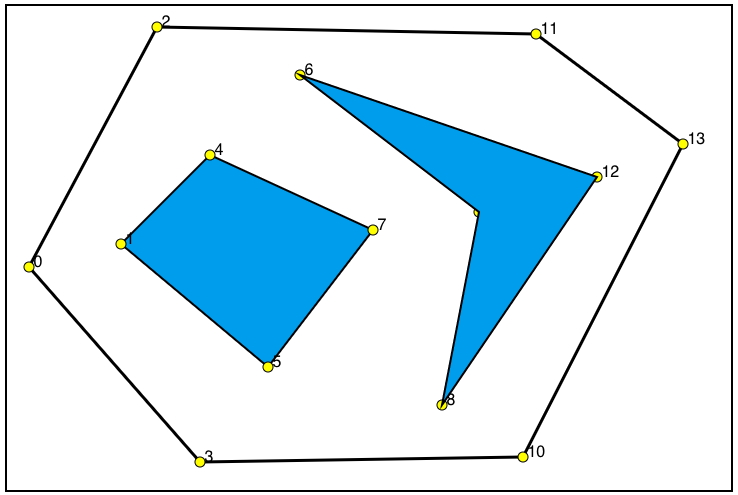
Figure 2-Vertex points of polygons are marked

To obtain decomposition, at each vertex V, we draw two edge segments one is called upper extension and the other is called lower extension. In the Fig.3 below, upper and lower edge extensions are depicted as red and blue lines respectively. As you can realize, some of the polygon vertices have only upper part, some of them have only lower and some have both parts.


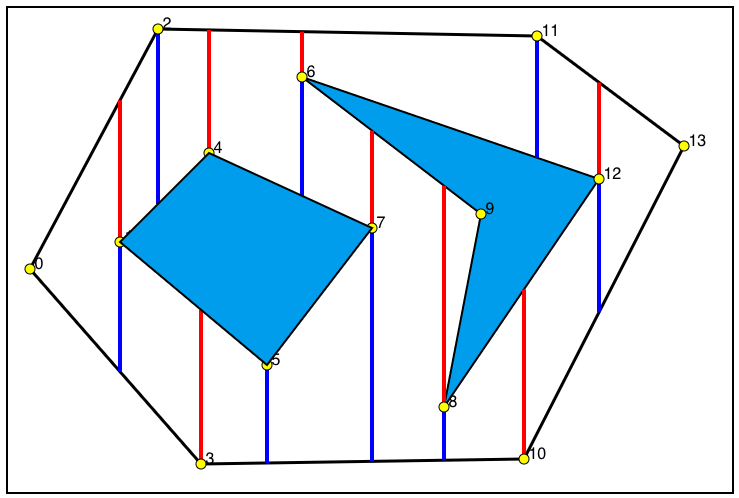
Figure 3-Upper and lower edge extensions of a polygon vertex is depicted.

How to determine trapezoidal cells?

Each trapezoidal cell lies betwen two successive polygon vertex. For two vertices to be successive, they must be visible and they must be successive as numerical value also. For example, V1 and V2 is visible, so we can determine that region as a cell whose borders are the red and blue edges extended by V1 and V2. V2 and V3 are not visible, so we can not create a cell between them, then we look for V2 and V4 to create a cell and it is ok. That means, we are looking for the first available successive of vertex. Note that, if a vertex is not the last vertex (here it is V13) there must be its successive to create a cell.

In summary, what we do exactly do is to determine a trapezoidal cell, finding successive polygon vertexs. This process may become sometimes so easy as V2 and V4. For instance, for a V6, there are 4 successives V7, V8, V11 and V13. Since V6 is a seperating vertex which means seperating region into two distinct regions we have to select two successives. From the upper part V11 is selected and from the lower part V7 is selected. From here we can understand that, classifying polygon vertex as 'in' (e.q. V6), 'middle' (e.q. V4) and 'out' (e.q. V7) is a good idea for some purposes.


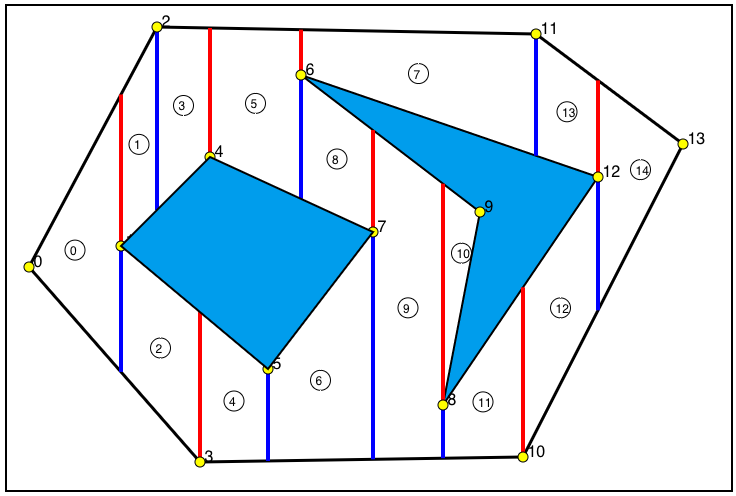
Figure 4-Deteremined Trapezoidal Cells.

After creation of trapezoidal cells, it is time to create their adjacency graph. Adjacency graph is created using their commong edges. For instance, C5 (cell with number 5) and C7 are adjacent since they share common vertex V6. C5 and C8 are also adjacent because of the same reason.


Figure 5-Adjacency graph of trapezoidal cells.

How to determine vertex positions for path planning?

An A* algorithm can find a optimal path using this graph. There are some posibilities for creating a path actually, one is connecting center of each cell, another is connecting middle point of each edge of trapezoidal cells's. Actually connecting center of trapezoidals is not a good idea, since it can cause that path coincides with obstacle like in the example of C9 and C11 in the Fig.7. When we try to connect them it intersects with the lower part of the obstacle. Therefore selecting middle points of trapezoid edges is better way for avoiding obstacles.


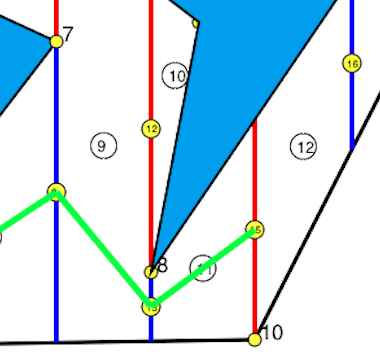
Figure 6-Vertexes are located at the middle of cell edges


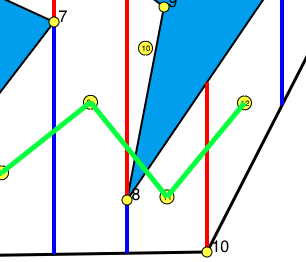
Figure 7-Vertexes are located at the center of the cell.

A* shortest path algorithm finds shortest path between two vertices. Algorithm is actually complete. If a path exist it eventually finds. Even if it is the shortest path along vertices, but it does not guarentee that it is actually the shortest. Because path is strictly depends on the vertex positions. You can see an example below in Fig. 8.


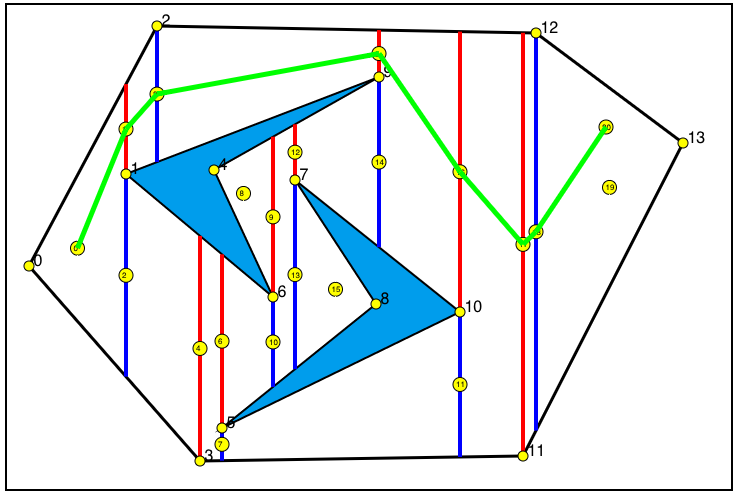
Figure 8-Longer path because of vertex positions


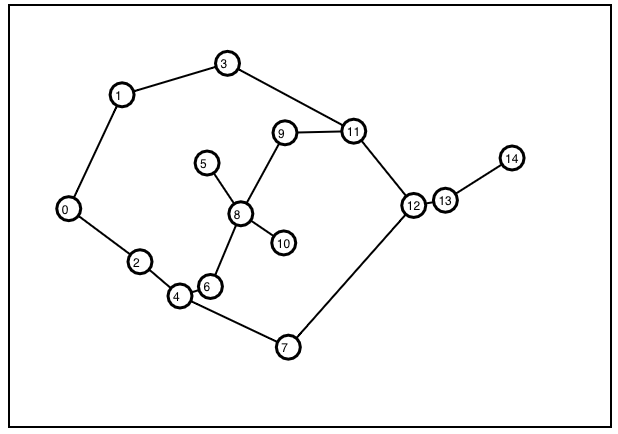
Figure 9-Corresponding adjacency graph of Fig.8.

Cell Coverage

Coverage of a cell means that traversing all free space cell by cell. For the simplicity and efficiency trapezoidal cells are merged if possible. These newly created cells are called Boustrophedon Cell. For the coverage problem, instead of starting a coverage from each cell starting position (causes eficiency loss), continuing exactly where previous cell coverage ended is a better way for coverage.

If we compare with old decomposition, we can easily realize that we have less trapezoid cells in Fig.9 compared to that of Fig.4.


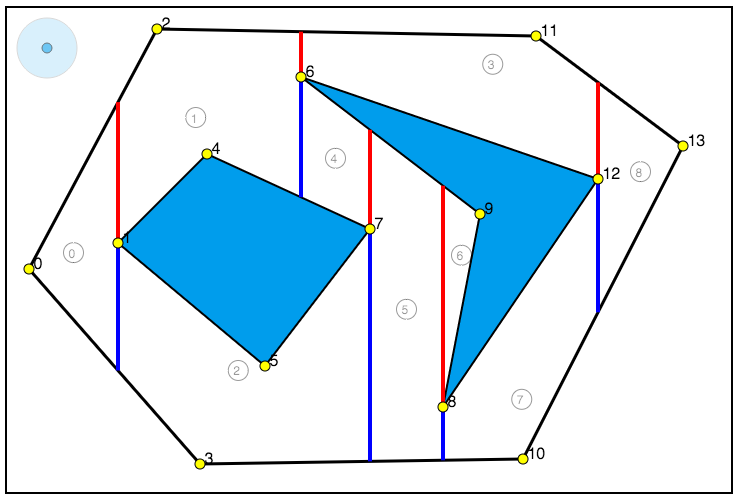
Figure 9-Boustrophedon Cells of Fig.4


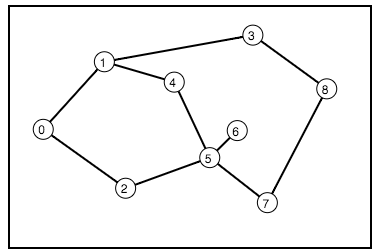
Figure 10-Corresponding adjacency graph of Fig.9.

For realizing cell coverage, our robot has to realize obstacles, therefore we used tangent bug robot has laser range scanner. Starting from left-top part of the each cell it goes down until it reaches right-down part of the cell. If tangent bug robot goes down it checks lasers positioned at bottom part, if it goes up it checks lasers positioned at up part. When tangent bug robot touches up or down part, it changes its mode to boundary following mode. After follow boundary some certain length, it goes other side of the cell.

Cell covering is applied subsequently in depth first traversal manner. Starting from trapezoid cell 0, then 1->3->8->7->5->6->2->4. Breadt-first type traversals are actually is less efficient in this kind of setup. Cell 0 then going up (1) and down (2) takes much effort and time.


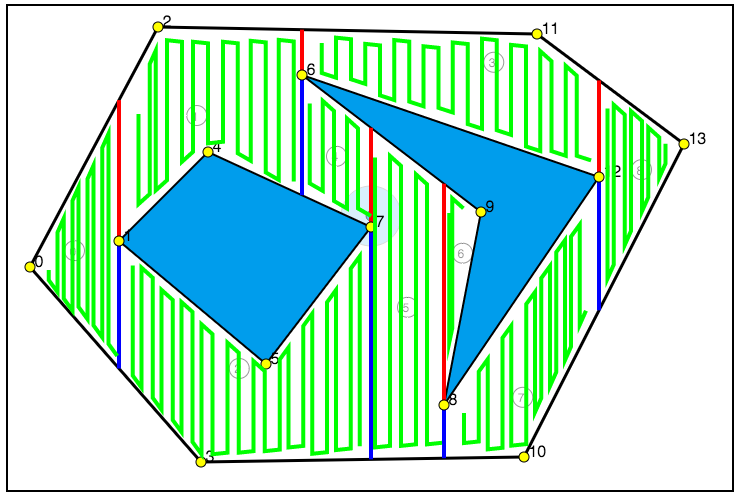
Figure 11-Cell Coverage of trapezoidal cells

Discussion

This homework is coded on Javascript with PaperJs Library and JQuery libraries. Performance of cell decomposition and cell coverage part are strongly depend on client computer, since they are running on your computer. Empirically, cell decomposition part takes 50 miliseconds on dual core processor with 2 gb ram. So it is real time wen you move polygons or polygon vertex. However, Coverage part takes about 3-5 seconds with the same computer. (Polygons are considered as above)

For this assignment Javasript is deliberately selected cause it is really easy to do some vector mathematics and math calculations with some libraries. Furthermore, javascript enables object-oriented type coding which makes more complex object relations easier. Because in this assignment, vertexes, edges, cells are all objects and they are interacted, some include others.